Florent Leclercq

Chargé de recherche CNRS, Institut d'Astrophysique de Paris


Blog

Evolution of cosmological simulations over the last 50 years

08-04-2020

I recently scanned the literature for the purpose of following and plotting the number of particles used in \(N\)-body simulations over the last five decades.

Direct summation simulations

Cosmological simulations started with as few as 100 particles just before 1970. Until particle-mesh methods became popular in the 1980s, "direct summation", i.e. explicit computation of all gravitational interactions between pairs of particles, was the preferred method [1-7]. Direct summation is now mostly used in the context of simulating star clusters or the Galactic centre, with detailed interactions between stellar systems and the central supermassive black hole [30,36,45,56]. The number of particles used in some of these simulations is presented in figure 1.

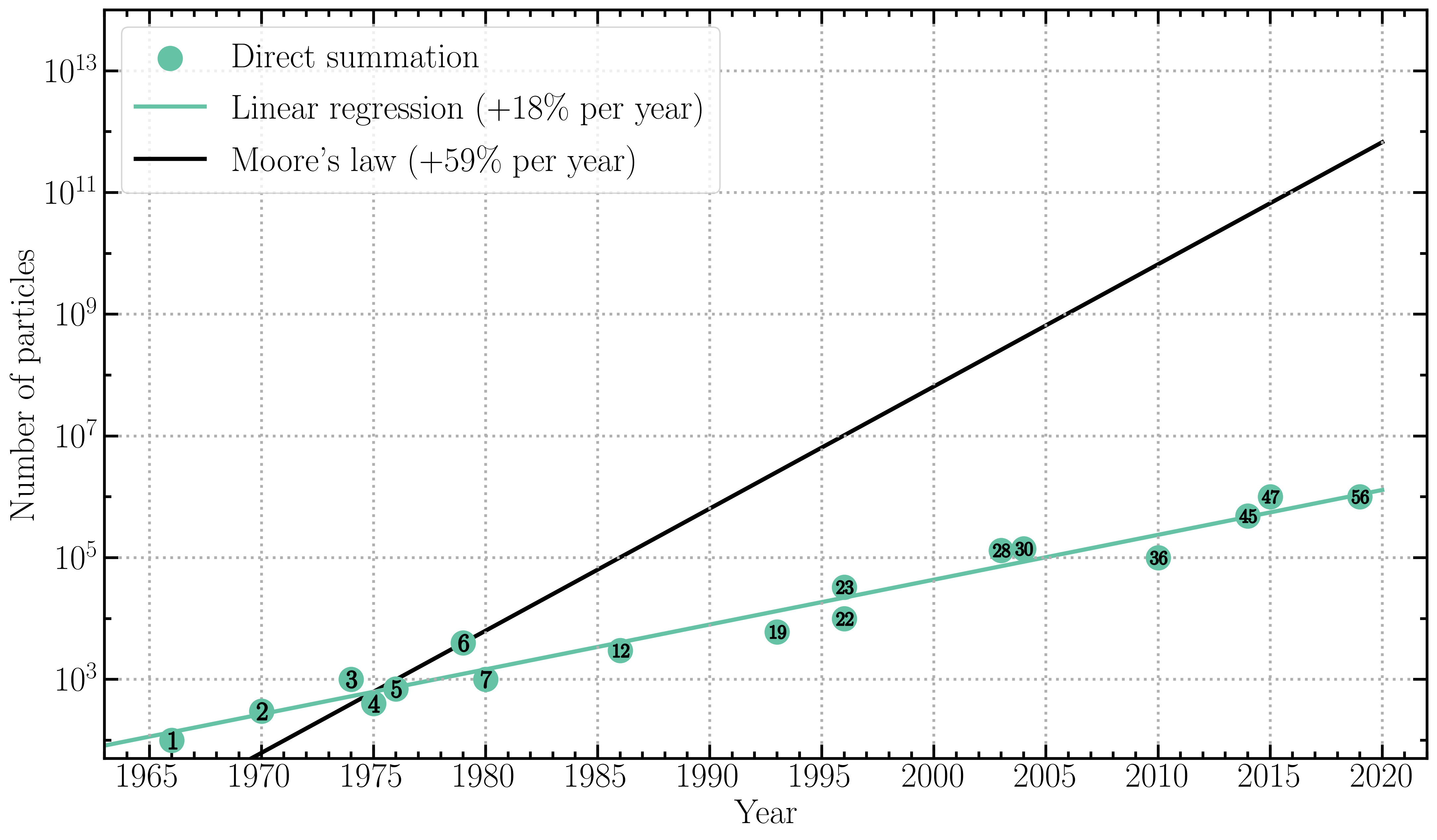Number of particles in direct summation simulations as a function of timeFigure 1: Evolution of the number of particles used in direct \(N\)-body simulations as a function of year of publication. The green line shows the trend as compared to Moore's law for hardware performance (black line).

Direct \(N\)-body methods scale as \(\mathcal{O}(N^2)\). For this reason, despite the enhancement provided by the use of accelerators such as GPUs [see e.g. 47], it is understandable that the number of particles does not follow Moore's law. A linear regression of \(\log N\) shows that \(N\) increases by around 18% per year, as compared to 59% per year for computer chip performance, which roughly doubles every 18 months according to Moore's law.

Sofware improvements

In order to circumvent the problem of the long-range nature of gravitational interactions, much of the work on numerical cosmology since 1980 has focused on algorithms (such as mesh, tree, and multipole methods) that reduce the need for communications across the full computational volume. The number of particles in some \(N\)-body simulations run using such techniques is plotted in figure 2, with the symbol and colour indicating the technique employed: particle-particle-particle-mesh (P3M) and adaptive P3M (AP3M); parallel or vectorized P3M; Tree; TreePM; and particle-mesh with adaptive mesh refinement (PM AMR).

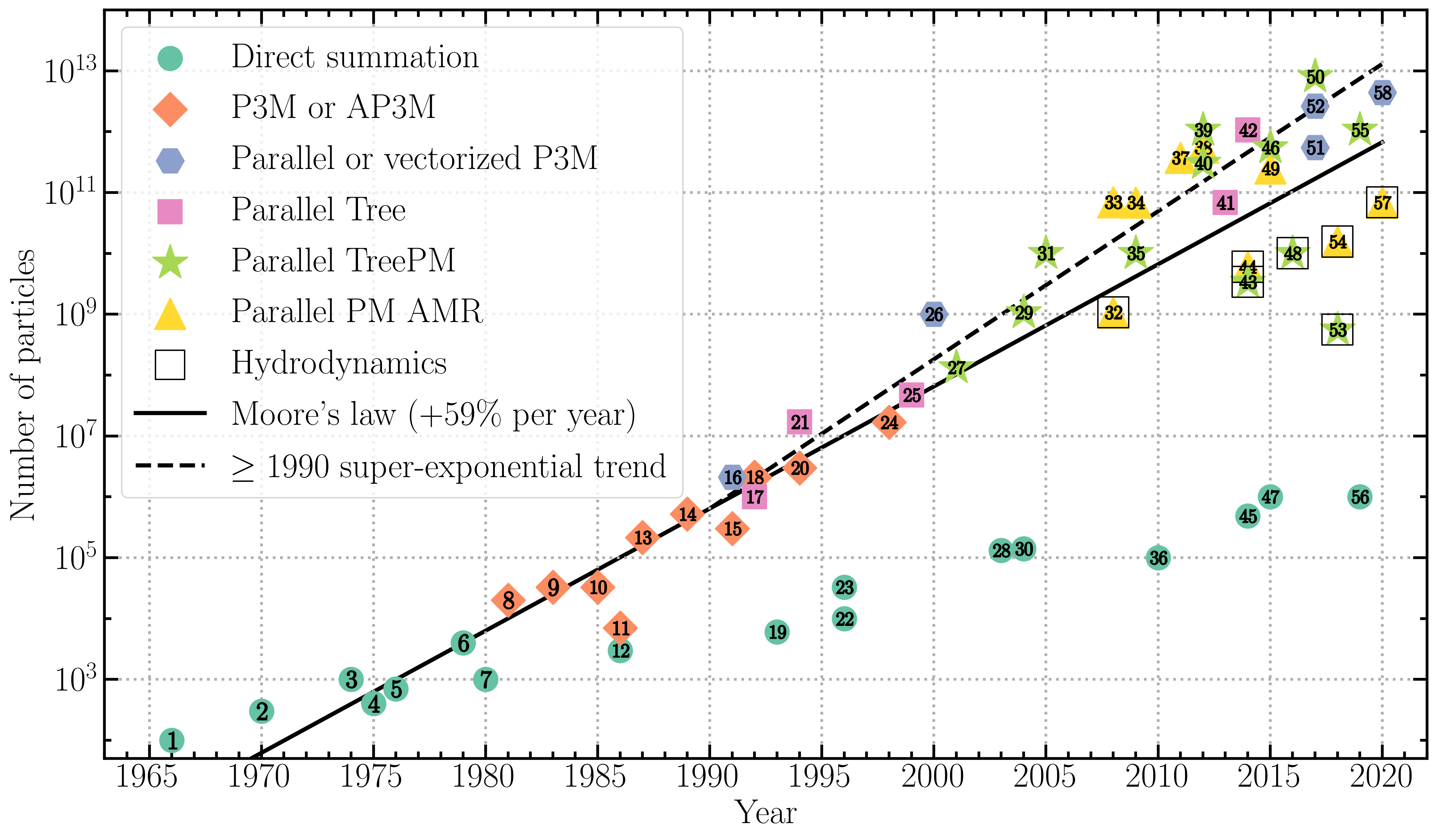Number of particles in direct summation simulations as a function of timeFigure 2: Evolution of the number of particles used in \(N\)-body simulations as a function of year of publication. The symbols and colours indicate the technique used for gravity. Hydrodynamic simulations are represented in a black square.

Because of software improvements the number of particles in cosmological simulations has increased much more rapidly than with the direct summation method. Since 1990, a super-exponential trend can further be observed for gravity-only simulations (it is illustrated by a quadratic regression of \(\log N\) in figure 2). It cannot be explained only by the increase in computer speed.

Downloading, reproducing, and citing these plots

The latest versions of the above plots are available to download from a Github repository made public along with this blog post:

  • Main plot, with all the data points: [pdf] [png]
  • Direct summation data points only: [pdf] [png]
  • Direct summation data points, linear regression, and Moore's law: [pdf] [png]
  • All data points and Moore's law: [pdf] [png]
  • All data points, Moore's law, and quadratic regression of gravity-only data points: [pdf] [png]

These plots can be reproduced using this Jupyter notebook. The references for all of the data points are listed below, and the latest bibliography is also provided in an ASCII file which can be easily loaded with python:

import numpy as np
A=np.loadtxt("references.txt",dtype={'names': ('id','authors', 'year', 'N', 'physics',
'method', 'ref'), 'formats': ('i4','S1000', 'i4', 'i8', 'S8', 'S8', 'S1000')},
delimiter=" ; ")

You can use all of these products freely, but giving credit, for instance by citing this blog post (http://florent-leclercq.eu/blog.php?page=2) and/or the address of the companion Github repository (https://github.com/florent-leclercq/Moore_law_cosmosims), would be appreciated. Everything is provided under the GNU General Public License version 3.

To submit corrections or updates, please do not hesitate to contact me using my usual email address, or to fork the Github repository and create pull requests.

References

  • [1] S. J. Aarseth, Dynamical evolution of small stellar systems, IAU Symposium No. 25 (1966) (\(N=100\), Gravity, Direct summation)
  • [2] P. J. E. Peebles, Structure of the Coma Cluster of Galaxies, AJ 75, 13 (1970) (\(N=300\), Gravity, Direct summation)
  • [3] W. H. Press & P. Schechter, Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation, ApJ 187, 425 (1974) (\(N=1,000\), Gravity, Direct summation)
  • [4] K. Miyoshi & T. Kihara, Development of the correlation of galaxies in an expanding universe, PASJ 27, 333 (1975) (\(N=400\), Gravity, Direct summation)
  • [5] S. D. M. White, The dynamics of rich clusters of galaxies, MNRAS 177, 717 (1976) [ADS] (\(N=700\), Gravity, Direct summation)
  • [6] S. J. Aarseth, J. R. Gott III & E. L. Turner, N-body simulations of galaxy clustering. I. Initial conditions and galaxy collapse times, ApJ 228, 664 (1979) (\(N=4,000\), Gravity, Direct summation)
  • [7] E. Terlevich, N-Body Simulations of Open Clusters, IAU Symposium No. 85 (1980) (\(N=1,000\), Gravity, Direct summation)
  • [8] G. Efstathiou & J. W. Eastwood, On the clustering of particles in an expanding universe, MNRAS 194, 503 (1981) [ADS] (\(N=20,000\), Gravity, P3M)
  • [9] S. D. M. White, C. S. Frenk & M. Davis, Clustering in a neutrino-dominated universe, ApJ Letters 274, L1 (1983) (\(N=2^{15}\), Gravity, P3M)
  • [10] M. Davis, G. Efstathiou, C. S. Frenk & S. D. M. White, The evolution of large-scale structure in a universe dominated by cold dark matter, ApJ 292, 371 (1985) (\(N=2^{15}\), Gravity, P3M)
  • [11] P. J. Quinn, J. K. Salmon & W. H. Zurek, Primordial density fluctuations and the structure of galactic haloes, Nature 322, 329 (1986) [ADS] (\(N=7,000\), Gravity, P3M)
  • [12] S. Inagaki, Post-collapse evolution of globular clusters with finite number of stars in the core, PASJ 38, 853 (1986) (\(N=3,000\), Gravity, Direct summation)
  • [13] S. D. M. White, C. S. Frenk, M. Davis & G. Efstathiou, Clusters, Filaments, and Voids in a Universe Dominated by Cold Dark Matter, ApJ 313, 505 (1987) (\(N=216,000\), Gravity, P3M)
  • [14] R. G. Carlberg & H. M. P. Couchman, Mergers and Bias in a Cold Dark Matter Cosmology, ApJ 340, 47 (1989) (\(N=2^{19}\), Gravity, P3M)
  • [15] J. Dubinski & R. G. Carlberg, The Structure of Cold Dark Matter Halos, ApJ 378, 496 (1991) (\(N=300,000\), Gravity, P3M)
  • [16] Y. Suto & T. Suginohara, Redshift-Space Correlation Functions in the Cold Dark Matter Scenario, ApJ Letters 370, L15 (1991) (\(N=128^3\), Gravity, parallel P3M)
  • [17] M. S. Warren, P. J. Quinn, J. K. Salmon & W. H. Zurek, Dark Halos Formed via Dissipationless Collapse. I. Shapes and Alignment of Angular Momentum, ApJ Letters 399, 405 (1992) (\(N=1,000,000\), Gravity, Tree)
  • [18] H. M. P. Couchman & R. G. Carlberg, Large-Scale Structure in a Low-Bias Universe, ApJ 389, 453 (1992) (\(N=128^3\), Gravity, P3M)
  • [19] S. J. Aarseth & D. C. Heggie, A 6000-Body Simulation with Primordial Binaries, PASP (1993) (\(N=6,000\), Gravity, Direct summation)
  • [20] J. M. Gelb & E. Bertschinger, Cold Dark Matter. I. The Formation of Dark Halos, ApJ 436, 467 (1994) (\(N=144^3\), Gravity, P3M)
  • [21] W. H. Zurek, P. J. Quinn, J. K. Salmon & M. S. Warren, Large-Scale Structure after COBE: Peculiar Velocities and Correlations of Cold Dark Matter Halos, ApJ Letters 431, 559 (1994) (\(N=17,154,598\), Gravity, Tree)
  • [22] R. Spurzem & S. J. Aarseth, Direct collisional simulation of 10000 particles past core collapse, MNRAS 282, 19 (1996) [ADS] (\(N=10,000\), Gravity, Direct summation)
  • [23] J. Makino, Postcollapse Evolution of Globular Clusters, ApJ 471, 796 (1996) [ADS] (\(N=2^{15}\), Gravity, Direct summation)
  • [24] A. Jenkins et al., Evolution of structure in cold dark matter universes, ApJ 499, 20 (1998) [ADS] (\(N=256^3\), Gravity, P3M)
  • [25] F. Governato et al., Properties of galaxy clusters: mass and correlation functions, MNRAS 307, 949 (1999) [ADS] (\(N=47,000,000\), Gravity, Tree)
  • [26] J. M. Colberg et al., Clustering of galaxy clusters in cold dark matter universes, MNRAS 319, 209 (2000) [ADS] (\(N=10^9\), Gravity, parallel P3M)
  • [27] P. Bode, N. A. Bahcall, E. B. Ford & J. P. Ostriker, Evolution of the Cluster Mass Function: Gpc3 Dark Matter Simulations, ApJ 551, 15 (2001) [ADS] (\(N=512^3\), Gravity, TreePM)
  • [28] H. Baumgardt & J. Makino, Dynamical evolution of star clusters in tidal fields, MNRAS 340, 227 (2003) [ADS] (\(N=131,028\), Gravity, Direct summation)
  • [29] J. Wambsganss, P. Bode & J. P. Ostriker, Giant Arc Statistics in Concord with a Concordance Lambda Cold Dark Matter Universe, ApJ Letters 606, L93 (2004) [ADS] (\(N=1024^3\), Gravity, TreePM)
  • [30] S. F. Portegies Zwart et al., Formation of massive black holes through runaway collisions in dense young star clusters, Nature 428, 724 (2004) [ADS] (\(N=140,000\), Gravity, Direct summation)
  • [31] V. Springel et al. (Millenium), Simulations of the formation, evolution and clustering of galaxies and quasars, Nature 435, 629 (2005) [ADS] (\(N=2160^3\), Gravity, TreePM)
  • [32] P. Ocvirk, C. Pichon & R. Teyssier (Horizon-MareNostrum), Bimodal gas accretion in the Horizon-MareNostrum galaxy formation simulation, MNRAS 390, 1326 (2008) [ADS] (\(N=1024^3\), Hydro, AMR)
  • [33] J. Kim, C. Park, J. R. Gott III & J. Dubinski, (Horizon Run 1), The Horizon Run N-Body Simulation: Baryon Acoustic Oscillations and Topology of Large-scale Structure of the Universe, ApJ 701, 1547 (2009) [ADS] (\(N=1024^3\), Gravity, AMR)
  • [34] R. Teyssier et al. (Horizon-4Pi), Full-sky weak-lensing simulation with 70 billion particles, A&A 497, 335 (2009) [ADS] (\(N=4096^3\), Gravity, AMR)
  • [35] R. E. Angulo, C. G. Lacey, C. M. Baugh & C. S. Frenk, The fate of substructures in cold dark matter haloes, MNRAS 399, 983 (2009) [ADS] (\(N=2160^3\), Gravity, TreePM)
  • [36] J. R. Hurley & A. D. Mackey, N-body models of extended star clusters, MNRAS 408, 2353 (2010) [ADS] (\(N=100,000\), Gravity, Direct summation)
  • [37] J. Kim, C. Park, G. Rossi, S. M. Lee, & J. R. Gott III (Horizon Runs 2 & 3), The New Horizon Run Cosmological N-Body Simulations, JKAS 44, 217 (2011) [ADS] (\(N=7210^3\), Gravity, AMR)
  • [38] J-M. Alimi et al. (DEUS-FUR), DEUS Full Observable ΛCDM Universe Simulation: the numerical challenge (2012) [ADS] (\(N=8192^3\), Gravity, AMR)
  • [39] T. Ishiyama, K. Nitadori & J. Makino, 4.45 Pflops Astrophysical N-Body Simulation on K computer -- The Gravitational Trillion-Body Problem (2012) [ADS] (\(N=10240^3\), Gravity, TreePM)
  • [40] R. E. Angulo et al. (Millenium-XXL), Scaling relations for galaxy clusters in the Millennium-XXL simulation, MNRAS 426, 2046 (2012) [ADS] (\(N=6720^3\), Gravity, TreePM)
  • [41] M. S. Warren, 2HOT: An Improved Parallel Hashed Oct-Tree N-Body Algorithm for Cosmological Simulation (2013) [ADS] (\(N=4096^3\), Gravity, Tree)
  • [42] S. W. Skillman et al. (Dark Sky), Dark Sky Simulations: Early Data Release (2013) [ADS] (\(N=10240^3\), Gravity, Tree)
  • [43] J. Schaye et al. (EAGLE), The EAGLE project: simulating the evolution and assembly of galaxies and their environments, MNRAS 446, 521 (2015) [ADS] (\(N=1504^3\), Hydro, TreePM)
  • [44] M. Vogelsberger et al. (Illustris), Properties of galaxies reproduced by a hydrodynamic simulation, Nature 509, 177 (2014) [ADS] (\(N=1820^3\), Hydro, TreePM)
  • [45] D. C. Heggie, Towards an N-body model for the globular cluster M4, MNRAS 445, 3435 (2014) [ADS] (\(N=484,710\), Gravity, Direct summation)
  • [46] T. Ishiyama et al. (ν2GC), The ν2GC simulations: Quantifying the dark side of the universe in the Planck cosmology, PASJ 67, 61 (2015) [ADS] (\(N=8192^3\), Gravity, TreePM)
  • [47] L. Wang et al., NBODY6++GPU: ready for the gravitational million-body problem, MNRAS 450, 4070 (2015) [ADS] (\(N=1,000,000\), Gravity, Direct summation)
  • [48] A. Fattahi et al. (APOSTLE), The APOSTLE project: Local Group kinematic mass constraints and simulation candidate selection, MNRAS 457, 844 (2016) [ADS] (\(N=2160^3\), Hydro, TreePM)
  • [49] J. Kim, C. Park, B. L'Huillier & S. E. Hong (Horizon Run 4), Horizon Run 4 Simulation: Coupled Evolution of Galaxies and Large-Scale Structures of the Universe, JKAS 48, 213 (2015) [ADS] (\(N=6300^3\), Gravity, AMR)
  • [50] D. Potter, J. Stadel & R. Teyssier, PKDGRAV3: beyond trillion particle cosmological simulations for the next era of galaxy surveys, ComAC 4, 2 (2017) [ADS] (\(N=8\times 10^{12}\), Gravity, TreePM)
  • [51] K. Heitmann et al. (Q Continuum), HACC Cosmological Simulations: First Data Release, ApJS 244, 17 (2017) [ADS] (\(N=8192^3\), Gravity, parallel P3M)
  • [52] H-R. Yu et al. (TianNu), Differential neutrino condensation onto cosmic structure, Nature Astronomy 1, 0143 (2017) [ADS] (\(N=13824^3\), Gravity, parallel P3M)
  • [53] P. F. Hopkins et al. (FIRE-2), FIRE-2 simulations: physics versus numerics in galaxy formation, MNRAS 480, 800 (2018) [ADS] (\(N=5.6 \times 10^8\), Hydro, TreePM)
  • [54] A. Pillepich et al. (IllustrisTNG), First results from the IllustrisTNG simulations: the stellar mass content of groups and clusters of galaxies, MNRAS 475, 648 (2018) [ADS] (\(N=2500^3\), Hydro, AMR)
  • [55] K. Heitmann et al. (Outer Rim), The Outer Rim Simulation: A Path to Many-core Supercomputers, ApJS 245, 16 (2019) [ADS] (\(N=10240^3\), Gravity, TreePM)
  • [56] T. Panamarev et al., Direct N-body simulation of the Galactic centre, MNRAS 484, 3279 (2019) [ADS] (\(N=1,000,000\), Gravity, Direct summation)
  • [57] M. Trebitsch et al. (Obelisk), The Obelisk simulation: galaxies contribute more than AGN to HI reionization of protoclusters, A&A 653, A154 (2021) [ADS] (\(N=4096^3\), Hydro, AMR)
  • [58] S. Cheng et al. (Cosmo-π), CUBE -- Towards an Optimal Scaling of Cosmological N-body Simulations (2020) [ADS] (\(N=16384^3\), Gravity, parallel P3M)